D2L_Ch01_深度学习的相关概念
机器学习训练的主要流程:
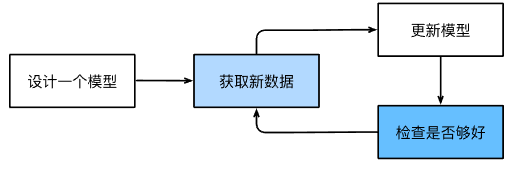
机器学习中的关键组件⚙
| ⚙组件 | 注释 | |
| 📊数据 | 数据集由一个个样本(example, sample)组成;遵循独立同分布(independently and identically distributed, i.i.d.);每个样本由一组称为特征(features,或协变量(covariates))的属性组成。 机器学习模型会据此性进行预测;数据集包括训练集(training dataset)、验证集(val dataset)和测试集(test dataset)。 | |
| 📐 模型 | 模型是用来转换数据的,由神经网络错综复杂地交织在一起。 | |
| 🎯 目标函数 | 也被称为“损失函数”,用来量化模型的有效性。大多数情况是“可优化”的; 预测数值时,最常见的损失函数是平方误差(squared error),即预测值与实际值之差的平方; 解决分类问题时,最常见的目标函数是最小化错误率,即预测与实际情况不符的样本比例。 |
|
| 🗝 优化算法 | 用于搜索最佳参数,以最小化损失函数。基本方法——梯度下降法(gradient descent) | |
各种机器学习问题
监督学习(supervised learning)
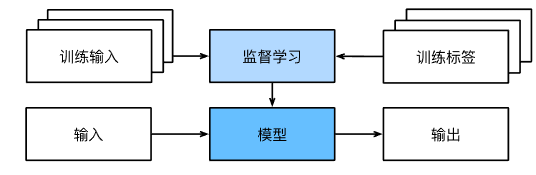
回归问题(regression)
任何有关“有多少”的问题很可能是回归问题,其目标是生成一个模型,使它的预测值非常接近实际标签值。
例如:你让人修理了排水管,承包商花了3小时清除污水管道中的污物,然后他寄给你一张350美元的账单。 而你的朋友雇了同一个承包商2小时,他收到了250美元的账单。 如果有人请你估算清理污物的费用,你可以假设承包商收取一些基本费用,然后按小时收费。 如果这些假设成立,那么给出这两个数据样本,你就已经可以确定承包商的定价结构:50美元上门服务费,另外每小时100美元。 在不经意间,你就已经理解并应用了线性回归算法。
分类问题(classification)
有关“哪一个”的问题很可能是分类问题,其目标是训练出一个分类器来预测样本属于哪个类别。
这类问题可以分为二项分类(binomial classification)和多项分类(binomial classification)两大类,其常见的损失函数被称为交叉熵(cross-entropy)
标注问题(Annotation)
有时我们希望模型描绘输入图像中的内容,比如:包含一只鸡、一只狗和一只猫。
学习预测不相互排次的类别的问题成为多标签分类(multi-label classification)
搜索问题(search)
搜索引擎会使用机器学习和用户行为来获取网页相关性的评分。
推荐系统(recommender system)
对于任何给定的用户,推荐系统都可以检索得分最高的对象集,然后推荐给用户。其缺陷在于:因为用户更倾向于给感觉强烈的参评打分,但所以单独使用其作为预测模型会导致数据中只包含“审查后的反馈”;因为系统会优先推送购买量较大的产品,所以可能会形成反馈循环。
序列学习(Sequence)
序列学习的输入样本是连续的,如:音频、视频等。我们期望训练的模型具有“记忆”功能,如视频样本,通过前一帧的图像,我们可能对后一帧中发生的事情更有把握。
❓问题 ❕注解 标记和解析 基于文本结构和语法假设对文本进行分解,以获得一些注释 自动语言识别 输入序列是说话人的录音,输出序列是说话人所说内容的文本记录 文本到语音 输入是文本,输出是音频文件 机器翻译 不同于语音识别,在机器翻译中颠倒输入输出的顺序非常重要。 虽然机器翻译也是将一个序转换成另一个序列,但输入和输出的数量以及相应序列的顺序大都不会相同
无监督学习(unsupervised Learning)
| ⚙问题 | 注解 | |
| 聚类(clustering) | 在没有标签的情况下,将样本分成某几大类,如:风景、动物、工具等。 | |
| 主成分分析(PCA) | 找少量的参数来准确捕捉数据的线性相关属性 | |
| 因果关系(CP) | 根据统计数据,来发现各类数据之间的关系 | |
| 生成对抗网络(GAN) | 一种合成数据的方法,甚至对于像图像和音频这样复杂的非结构化数据。 潜在的统计机制是检查真实数据和虚假数据是否相同的测试 |
|
强化学习(Reinforcement Learning)
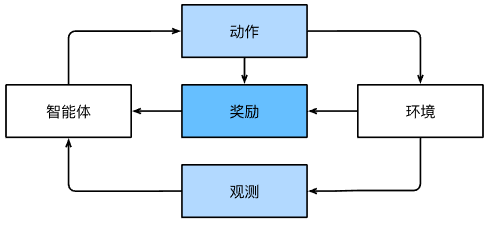
环境被完全观测的强化学习问题,称为马尔可夫决策过程(Markov decision process)
状态不依赖之前的动作,这类强化学习问题,称为上下文老虎机(contextual bandit problem)
只有一组最初未知奖励的可用动作的强化学习问题称为多臂老虎机(multi-armed bandit problem)








